4 插图和公式

Markdown 支持原生的插图和公式。也可以针对不同的输出格式，使用不同的插图和公式语法。

4.1 插图

在 Markdown 中，插入一张图片很简单，语法如下：

![](img/typesetting2.png)

图片默认会以页面大小 100%宽度显示，可以使用如下方法调整图片的宽度（这在长图片排版时非常有用，可以防止图片显示过大）：

![](img/typesetting2.png){ width=50% }

也可以插入带标题（caption）的图片，图片将会自动生成编号：

![这是一个有标题的图片](img/typesetting2.png){ width=50% }

可以在正文中引用图片，如图所示（注意，该方法在 docx 格式中不好用）。

![引用该图片\label{fig:typesetting}](img/typesetting2.png){ width=50% }

通过diagram-generator.lua，可以直接在 Markdown 中内嵌流程图。如下面的代码可以生成一个有向图：

```graphviz
digraph G {
    rankdir=LR
    r[color="red"]
    g[color="green"]
    b[color="blue"]
    r -> g -> b
}
```

也可以使用 Mscgen 画图，代码和图如下：

```msc
msc {
    alice, bob;

    alice -> bob[label="Hello World!"];
    bob -> alice[label="你好，世界！"];
}
```

可以给图片源加标题，如：

```{.graphviz caption="这是一张有标题的图片"}
digraph G {
    rankdir=LR
    a -> b -> c
}
```

注意：只有具有标题的图片才会自动生成图片编号。

也可以这样引用图片，如图所示。

```{.graphviz caption="\label{fig:example-1}这是另一张有标题的图片"}
graph G {
    rankdir=LR
    a -- b -- c
}
```

自 Pandoc 3.0 版（2023 年初发布）起，支持如下格式的语法（这样看起来更一致，可以与上面的写法对比其异同）：

```graphviz {caption="\label{fig:example-1}这是另一张有标题的图片"}
graph G {
    rankdir=LR
    a -- b -- c
}
```

我们使用自己搭的 Gitea¹服务器管理我们的 Markdown。为了能直接在 Web 界面上显示上述图片，我们写了一个浏览器插件：https://git.xswitch.cn/xswitch/giteaBar ，供大家参考。当然，团队中每个人都装插件比较麻烦，因此，我们弃用了上述插件，并自己定制了一版。

Github 已经支持使用 Mermaid²画图。直接使用如下语法即可。

```mermaid
graph TD;
    A-->B;
    A-->C;
    B-->D;
    C-->D;
```

但我们的 PDF 中暂时还不支持这个语法，主要是 Docker 镜像已经很大了，如果再加上 Mermaid，就会更大，而且，比起来，Mermaid 来的图并不怎么好看。

后来，我还学会了使用 Gnuplot³画图。下面的图是我画的圆与正弦波的图。以后有了时间，我也会讲讲我是怎么画的。

4.2 公式

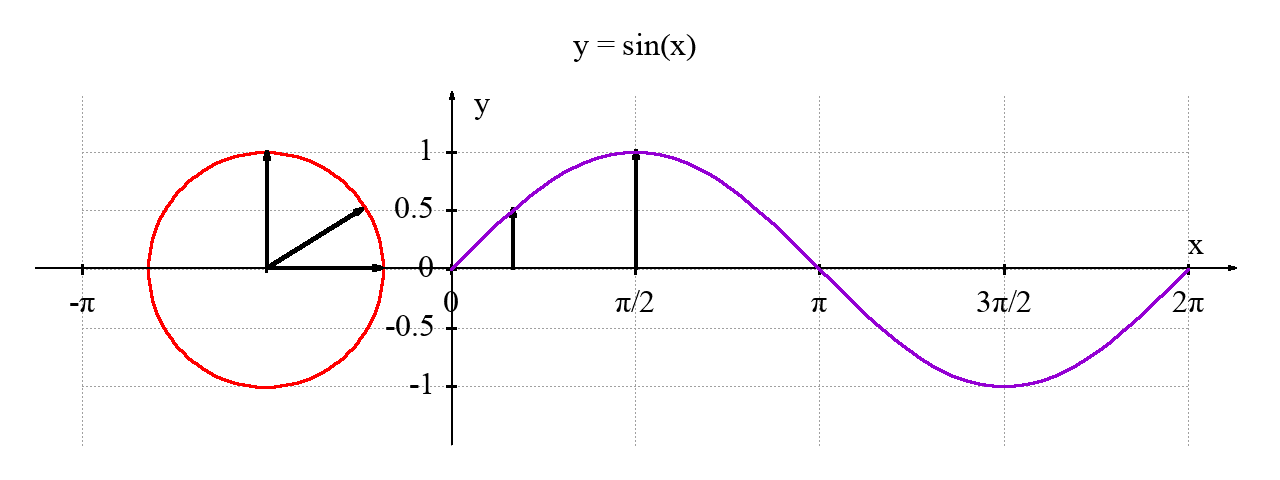
Markdown 支持行内公式，简单的公式可以使用原生的上下标格式写。上标写为x^2^，显示为 x²，下标写为x~2~，显示为 x₂，如著名的质能方程 E = mc²可以写为E = mc^2^。这种原生方式支持的输出格式比较多，如 HTML、PDF、docx等。如果公式比较复杂，也可以使用 Latex 语法的公式⁴，语法是$公式语法$，注意前$后面不要有空格，后$前面不要有空格。如$x^2 + y^2 = z^2$显示为$x^2 + y^2 = z^2$、$E = mc^2$显示为$E = mc^2$、欧拉公式$e^{i\pi} + 1 = 0$显示为$e^{i\pi} + 1 = 0$等。Latex 格式的公式对 PDF 支持比较好，docx中也可以正常显示，在 HTML 中有些能正常显示，有些需要配合 MathML 或 MathJax 生成公式。

也可以使用如下语法显示独立的公式（单独在一个段落中）：

$$
x^2 + y^2 = z^2
$$

$$x^2 + y^2 = z^2$$

在 PDF 中，配合diagram-generator.lua会对公式自动编号。

下面是一些公式示例，可以自行观察在不同输出格式（文件类型）中的效果。

\begin{equation}
\begin{aligned}
a &= b\\
a1 &= b1
\end{aligned}
\end{equation}

$$\begin{equation} \begin{aligned} a &= b\\ a1 &= b1 \end{aligned} \end{equation}$$

只有以下方式能出现在 docx 中，且公式在 docx 和 pdf 中都没有编号：

$$
\begin{aligned}
a &= b\\
a2 &= b2
\end{aligned}
$$

$$\begin{aligned} a &= b\\ a2 &= b2 \end{aligned}$$

下列公式在 PDF 中正常，在 docx 和 HTML 中不显示：

\begin{align}
a &= b\\
a3 &= b3
\end{align}

$$\begin{align} a &= b\\ a3 &= b3 \end{align}$$

\begin{align}
\begin{split}
a &= b\\
a4 &= b4
\end{split}
\end{align}

$$\begin{align} \begin{split} a &= b\\ a4 &= b4 \end{split} \end{align}$$

下面是一些有趣的公式：

$$
f(x)=\left\{\begin{align}
  1,x>0\\
  0,x=0\\
  -1,x<0
\end{align}\right.
$$

分段函数：

$$
f(x)=\left\{\begin{aligned}
  1,x>0\\
  0,x=0\\
  -1,x<0
\end{aligned}\right.
$$

$$f(x)=\left\{\begin{aligned} 1,x>0\\ 0,x=0\\ -1,x<0 \end{aligned}\right.$$

麦克斯韦方程组⁵：

$$
\begin{aligned}
    \nabla \cdot \mathbf{E} &= 4 \frac{\rho}{\varepsilon_0} \\
    \nabla \cdot \mathbf{B} &= 0 \\
    \nabla \times \mathbf{E} &= -\frac{\partial \mathbf{B}}{\partial t} \\
    \nabla \times \mathbf{B} &= \mu_0 \mathbf{J} + \frac{\partial \mathbf{E}}{\partial t}
\end{aligned}
$$

$$\begin{aligned} \nabla \cdot \mathbf{E} &= \frac{\rho}{\varepsilon_0} && 高斯定律\\ \nabla \cdot \mathbf{B} &= 0 && 高斯磁定律 \\ \nabla \times \mathbf{E} &= -\frac{\partial \mathbf{B}}{\partial t} && 法拉第电磁感应定律\\ \nabla \times \mathbf{B} &= \mu_0 \mathbf{J} + \mu_0\varepsilon_0\frac{\partial \mathbf{E}}{\partial t} && 麦克斯韦-安培定律 \end{aligned}$$

其中，如果把\frac替换为\cfrac，则在浏览器中不能正常显示。

麦克斯韦方程组的积分形式如下：

$$
\begin{aligned}
\oiint_{S} \, D\cdot ds &= Q_{f} \\
\oiint_{S} \, B \cdot ds &= 0 \\
\oint_{L} \, E \cdot dl &= -\frac{d \Phi B}{dt} \\
\oint_{L} \, H \cdot dl &= I_{f} + \frac{d \Phi D}{dt} \\
\end{aligned}
$$

$$\begin{aligned} \oiint_{S} \, D\cdot ds &= Q_{f} \\ \oiint_{S} \, B \cdot ds &= 0 \\ \oint_{L} \, E \cdot dl &= -\frac{d \Phi B}{dt} \\ \oint_{L} \, H \cdot dl &= I_{f} + \frac{d \Phi D}{dt} \\ \end{aligned}$$

矩阵：

$$\begin{pmatrix} a&b\\c&d \end{pmatrix} \quad \begin{bmatrix} a&b\\c&d \end{bmatrix} \quad \begin{Bmatrix} a&b\\c&d \end{Bmatrix} \quad \begin{vmatrix} a&b\\c&d \end{vmatrix} \quad \begin{Vmatrix} a&b\\c&d \end{Vmatrix}$$

求和：

$$f(x) \,\! = \sum_{n=0}^\infty a_n x^n = a_0+a_1x+a_2x^2+\cdots$$

付里叶级数：

$$F(t) = \frac{a_{0}}{2} + \sum_{n=1}^{\infty}[a_{n}cos(n \omega t) + b_{n}sin(n \omega t)]$$

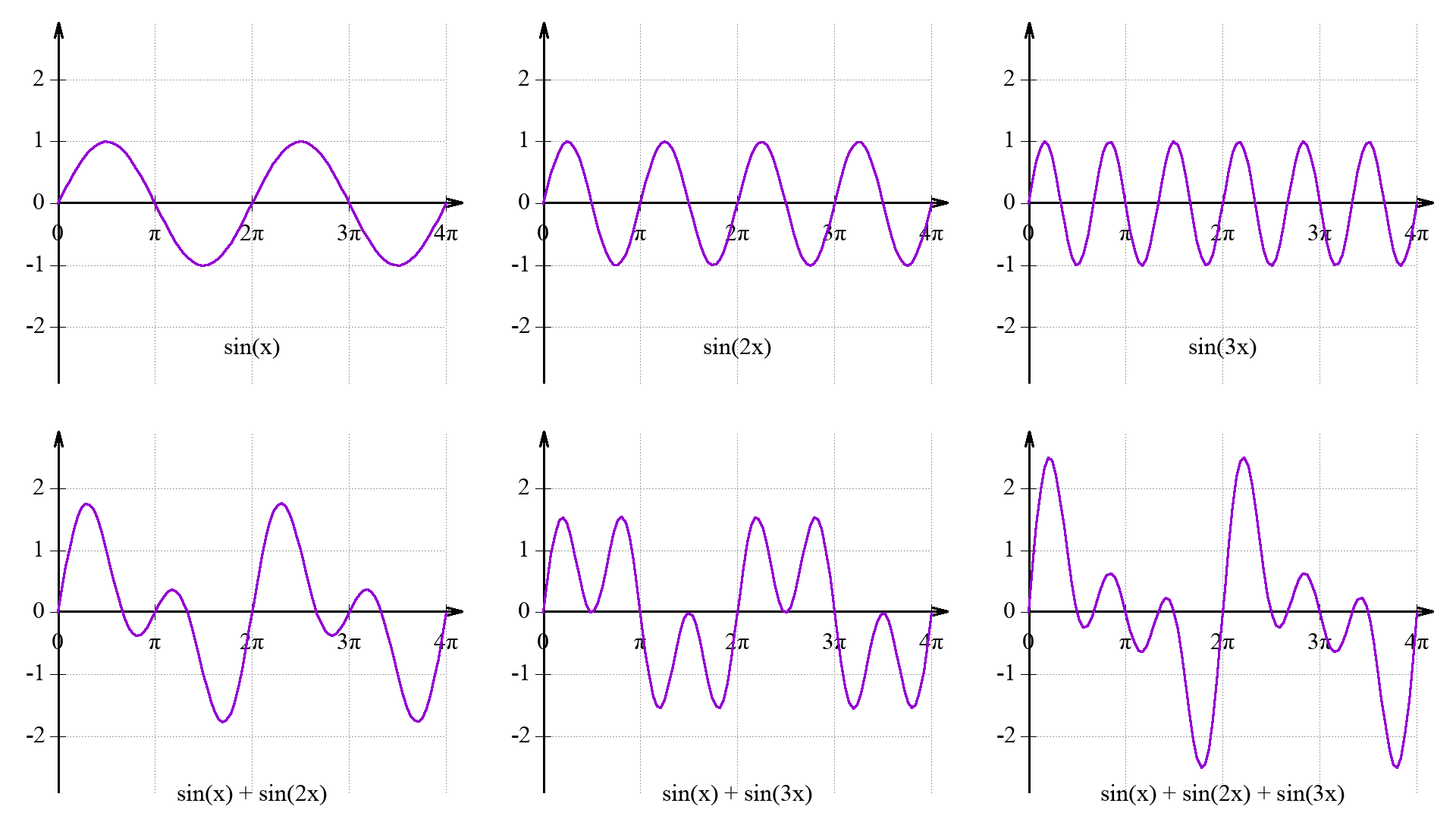
付里叶级数的复数形式：

$$\left\{ \begin{aligned} cos(n \omega t) &= \frac{e^{jn\omega t} + e^{-jn\omega t}}{2}\\ sin(n \omega t) &= \frac{e^{jn\omega t} - e^{-jn\omega t}}{2} \end{aligned} \right.$$

注：本节中的公式在不同的输出格式中不一定能正常显示，可以对比本书不同的版本如 HTML、PDF、docx等查看区别。